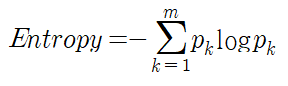까먹을까봐 적어놓는 블로그

 AdaBoost는 순차적으로 여러 개의 약분류기(weak classifier)를 결합시켜 하나의 강분류기를 구성하는 알고리즘으로 1996년 Freund와 Schapire가 제안한 부스팅 기법이다. 초기에는 모든 샘플에 대하여 동일한 가중치를 주고 약분류기를 학습시킨 뒤, 이전 분류기에서 잘못 분류된 샘플의 가중치를 크게함으로써 강분류기를 만들어가는 알고리즘이다.

 AdaBoost는 이진 분류(binary classification)에 최적화되어 있으며 학습자료가

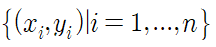
이고, 반응변수 y가

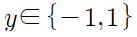
인 경우라고 하면, AdaBoost 알고리즘은 약분류기 f(x)들을 결합시켜 강분류기 F(x)를 마드는 과정이다.

여기서 α는 약분류기의 가중치인 최적계수이다.

구체적인 학습과정은 초기 샘플들의 가중치를

로 초기화 하고 가중치가 적용된 오류율 e를 구한다.

약분류기의 최적계수 α를 계산한다.

만약 무작위로 예측하여 오류율 e가 0.5에 가까워지면 (1-e)/e = 1이 되므로 약분류기의 가중치가 0에 가까워 지고, 오류율이 0.5보다 커지면 (1-e)/e < 1이 되어 약분류기의 가중치가 음수가  된다. 그 다음 모든 샘플의 부과하는 가중치를 

로 수정한다. 그런 다음 가중치들의 합이 1이 되도록 정규화 한다. 이 과정을 m = 1,...,M 번 반복하게 되면 약분류기 f에 의하여 잘못 분류된 샘플의 가중치를 높이는 방식으로 조정되게 된다.

 최종적으로 M단계 까지 적합된 강분류기 F(x)는

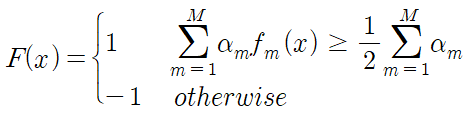
M개의 약분류기들의 선형결합으로 나타내어지며 다음 경계값 보다 큰 경우 1로 그렇지 않으면 -1로 분류하게 된다.

AdaBoost 적합 과정

CART(Calssification and Regression Trees, Beriman 1984) 알고리즘을 분류목적으로 사용하는 경우에는 불순도 측도로 지니 지수(Gini index)나 엔트로피(Entropy)를 사용한다.

지니 지수

엔트로피 지수

총 지니지수

연속형 변수를 두 개의 자식마디로 나누는 방법에는 다음과 같은 방법이 있다.

1. 모든 기준점으로 불순도 계산

2. 중위수, 사분위수를 기준으로 불순도 계산

3. 평균을 기준으로 불순도 계산

4. Class가 바뀌는 점을 기준으로 불순도 계산

여기서는 간단하게 위의 그림에서 나온대로 자식마디를 나누고 지니지수를 계산해보자.

 랜덤 포레스트(Random Forest)는 여러 개의 의사결정나무(Decision Tree)를 이용하여 높은 성능의 예측 모형을 만드는 앙상블 기법의 기계학습 방법이다. 앙상블 방법은 주어진 자료로부터 여러 개의 예측 모형을 구축한 후, 이 여러 모형의 예측 결과들을 종합하여 단순 다수결 투표를 통해 최종적으로 하나의 모형을 만들어 낸다. 이와 같이 여러 개의 의사결정나무를 사용해 만든 랜덤 포레스트는 한 개의 의사결정 나무를 사용하는 경우보다 정확성과 일반화 성능이 높다.

 랜덤 포레스트 알고리즘은 훈련 자료(Training set)로부터 B개의 부트스트랩(Bootstrap) 표본을 얻은 후 각각의 표본에 대해 p개의 설명 변수 중 m개를 랜덤하게 선택하여 의사결정 나무를 생성한다. 크게 훈련(training)단계와 검정(test) 단계로 나누어서 살펴보면, 훈련 단계에서는 먼저 중복을 허용하는 표본 추출 기법인 부트스랩 방법을 이용하여 크기가 N인 B개의 부트스트랩 표본을 생성한다. 이때 표본 추출 과정에서 선택되지 않은 표본을 OBB(Out-of-Bag)라고 한다. 그 후 p개의 설명 변수 중 m개를 무작위로 선택하여 의사결정나무를 생성한다. 이러한 과정을 B번 반복하게 되면 B개의 의사결정나무가 생성되며, 검정 단계에서는 훈련 단계에서 사용되지 않은 OBB들에 대하여 각각 B개의 의사결정나무를 적용여 OBB 에러를 측정한다.

 최종적으로 랜덤 포레스트는 B개의 다양한 의사결정나무 분류기(classifier)를 갖게 되고 새로운 표본이 입력되면 각 의사결정나무 분류기를 통해 예측된 class 중 가장 많이 득표한 class를 최종 예측으로 분류한다.

 랜덤 포레스트는 의사결정나무 생성 과정에서 랜덤하게 부트스트랩 표본을 추출하고 랜덤하게 변수들을 선택하는 과정을 반복하기 때문에 만들어지는 의사결정나무의 다양성을 높여준다. 이러한 랜덤 포레스트의 무작위성에 의해 서로 다른 특성을 갖는 의사결정나무들의 최종적인 투표를 통해 결정된 예측은 한 개의 의사결정나무를 사용하는 경우보다 정확성과 일반화 안정성이 더 좋다.

 랜덤포레스트 의사결정나무 생성 방법

 부트스트랩 표본을 구성하고 설명변수 p개 중 설명변수 m개를 랜덤하게 선택한다. 이때 선택하는 m은 보통 √p나 p/3을 선택한다. m개의 설명변수 중 가장 지니 지수(Gini index)를 작게하는 설명 변수와 분할 점을 선택하고 두 개의 자식 마디(daughter node)로 분할한다. 가지치기 없이 CART(Classification and Regression Trees, Brieman 1984) 알고리즘을 이용하여 의사결정나무를 생성하거나 또는 뿌리마디(root node)에서 끝마디(terminal node)까지의 깊이가 너무 크면 과적합이 발생할 수 있기 때문에 적절한 최소마디 크기를 정하여 의사결정나무를 생성한다.