$i$번째 개체의 생존시간 $T_i$는 서로 독립이고, 중도절단시간 $C_i$도 서로 독립이라고 하자. 그러면 관측시간 $Y_i=min(T_i, C_i)$이고 각각의 관측값은 $(Y_i, \delta _i)$로 대응하게 된다. 여기서 $\delta _i=0$이면 중도절단된 경우이고 $\delta _i=1$이면 중도절단 되지 않은 경우다. 시점 t를 넘어 생존할 확률을 나타내는 생존함수(survival function) $S(t)$는

이고, 시점 t까지는 생존했다가 시점 t 바로 직후에 사망하게 되는 순간 위험률을 나타내는 위험함수 $h(t)$는

로 정의된다.
T가 확률밀도함수 $f(x)$와 분포함수 $F(x)$를 갖는다고 하자. $S(t)$는 $S(0)=1, \lim _{t→∞}S(t)=0$이므로 생존함수 $S(t)$는

따라서 양변을 미분하면 $F(t)$는

또한, 생존함수 $f(x)$ 다음과 같이도 표현할 수 있다.

한편, 위험함수 $h(t)$는

$F(0)=1$을 이용하여 t에 대하여 적분하면 누적위험함수(culmulative harzard function) $H(t)$는

이므로 생존함수 $S(t)$는 누적위험함수 $H(t)$를 이용해 표현할 수 있다.

또한 위 식을 t에 대해 미분하면 생존함수 $f(t)$는 다음과 같이 표현할 수 있다.
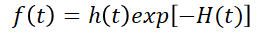
'생존분석' 카테고리의 다른 글
| [생존분석] 두 그룹에 대한 로그-순위 검정(log-rank test) (0) | 2020.07.05 |
|---|